Segment trees y Range minimum query- libreim

En los cursos de estructuras de datos y algoritmos el número de estructuras de datos que se suelen estudiar es bastante reducido. Generalmente se introducen heaps, árboles binarios de búsqueda balanceados (AVL), tablas Hash y algunos algoritmos sobre grafos. Sin embargo, el mundo de las estructuras de datos es mucho más amplio ¹ y probablemente requeriría una asignatura de estructuras de datos avanzadas como sucede en algunas universidades. El MIT, por ejemplo, proporciona vídeos con el contenido de esta asignatura. Por ello, intentaré escribir entradas en el blog que profundicen en esta temática.

En este caso trataremos los segment trees o árboles de segmentos. Introduciremos en primer lugar un problema importante de la teoría de algoritmos, range minimum query problem, que servirá como motivación para los segment trees. Posteriormente se explicará el funcionamiento de estos, proporcionando para cada operación su correspondiente código en Python. Por último, se proponen como ejercicio algunos problemas resolubles mediante segment trees.

Range Minimum Query Problem

Consideremos un vector con objetos de un tipo $T$ sobre el que se ha definido una relación de orden total. Por claridad, ejemplificaremos el problema sobre números enteros. Sea $n$ la longitud del vector, se define $RMQ(i,j)$ como el mínimo del subvector formado por las componentes entre $i$ y $j$ (inclusive) para $i, j$ en $\{0,\ldots,n-1\}$ con $i \le j$ . El problema consiste en proporcionar el valor de $RMQ(i,j)$ para cualquier número posible de consultas.

Normalmente se denomina subintervalo del vector a un subvector formado por componentes consecutivas, como los que se estudian en este caso. Una posible traducción al castellano de range minimum query problem sería problema de las consultas del mínimo de cualquier subintervalo (pero mantendremos el nombre en inglés por ser el estándar).

La solución trivial para el problema consiste en calcular para cada consulta el mínimo del subintervalo correspondiente de forma lineal. Esto proporciona una eficiencia media de $\theta(n)$ para las consultas. Se pretende reducir esta eficiencia significativamente para poder atender el mayor número de consultas posible.

La forma habitual de abordar el problema consiste en preprocesar los datos. Un primer preprocesamiento puede ser calcular directamente el mínimo para cada subintervalo del vector, lo que puede conseguirse sin mucha dificultad en $\theta(n^2)$ . Posteriormente, las consultas pueden ser realizadas en tiempo constante. Esta solución tiene dos grandes problemas:

Un preprocesamiento de eficiencia $\theta(n^2)$ es excesivo cuando se trate con vectores de tamaño mayor o igual que $10^4$ . Esto nos hace distinguir dos eficiencias a la hora de resolver el problema, la eficiencia del preprocesamiento y la eficiencia de la consulta. La solución trivial minimizaba el preprocesamiento mientras que la nueva solución minimiza el tiempo de consulta, no siendo ninguna de las dos óptimas.
El problema suele complicarse permitiendo actualizar el valor de una componente del vector entre consultas, lo que no consigue de forma eficiente el segundo algoritmo, que requiere un tiempo $\theta(n)$ para actualizar también la matriz $RMQ$ .

Los segment trees o árboles de segmentos surgieron para resolver este problema. Se pueden formular de forma incluso más general, teniendo aplicaciones en problemas relacionados con los subintervalos de un vector. Como veremos a continuación, los segment trees abordarán el range minimum query problem utilizando un preprocesamiento con eficiencia lineal tras el cual podremos realizar consultas y actualizar elementos del vector en tiempo logarítmico. Esto supone una gran mejora con respecto a las soluciones anteriores.

Segment Trees

Un segment tree es una estructura de datos que permite, a partir de un vector $V$ , dos operaciones:

Consultar determinada información para cualquiera de los subintervalos del vector.
Actualizar una componente del vector.

Como caso particular esta información puede ser el mínimo del subintervalo, en cuyo caso ambas operaciones pueden llevarse a cabo en tiempo logarítmico.

Supongamos por el momento que el vector tiene longitud $n = 2^m$ .

La idea subyacente consiste en preprocesar la información correspondiente a las particiones del vector formadas por subintervalos de igual longitud siendo esta una potencia de $2$ . Formalmente, estos intervalos se corresponden con $V[k2^l, (k+1)2^l-1]$ para $l \in \{0, 1, \ldots, m\}$ y $k \in \{0, 1, \ldots, \frac{n}{2^l}-1\}$ . Los intervalos preprocesados pueden verse como los nodos de un árbol binario construido de la siguiente forma:

$V[0,n-1]$ es la raíz.
Todo nodo que se corresponda a $V[i,j]$ con $i < j$ tiene dos hijos, izquierda y derecha, que se obtienen a dividir el subintervalo correspondiente en las mitades izquerda y derecha.

La Imagen 1 muestra el árbol binario a generar si se tuviese $n = 8$ . Nótese que las hojas del árbol son los subintervalos con una sola componente.

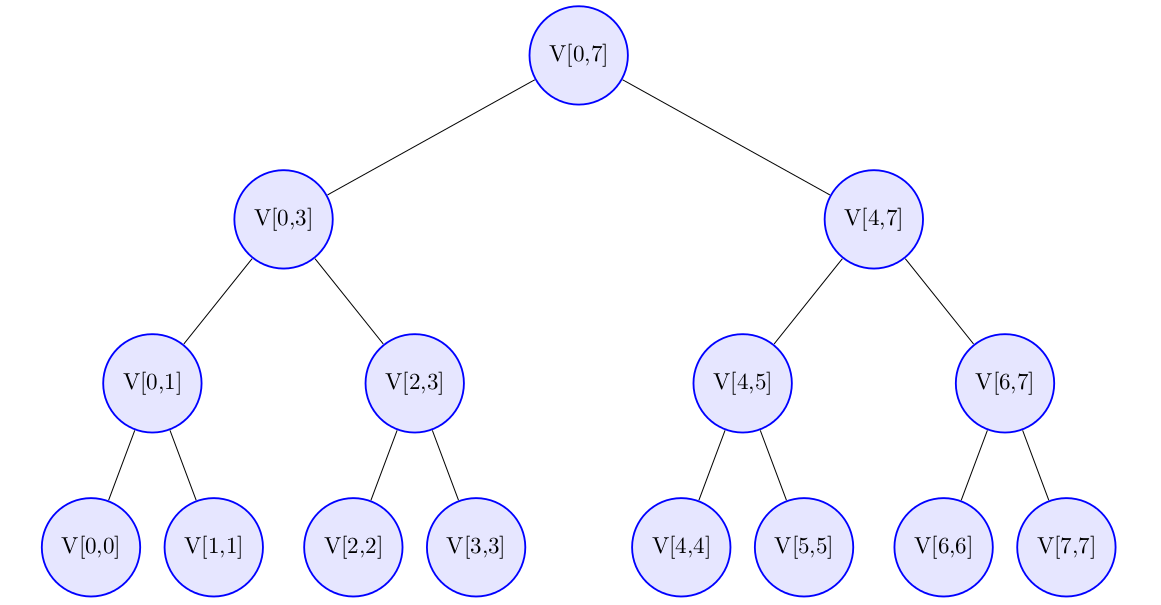Imagen 1. Segment tree asociado a un vector $V$ de longitud 8 representado como un árbol binario.

Tras generar el árbol binario podemos expresar un subintervalo $V[i, j]$ como la unión del menor número de subintervalos como los preprocesados previamente. Tiene sentido hablar de esta unión pues siempre existe (basta expresar $V[i, j]$ como unión de sus componentes). Por ejemplo, para $n=8$ se tiene:

$V[2,7] = V[2,2] +\mkern-5mu+ V[3,4] +\mkern-5mu+ V[5,6] +\mkern-5mu+ V[7,7]$

Si la información que deseamos consultar puede obtenerse a partir de la información de una partición de subintervalos entonces habremos resuelto el problema. Este es el caso del range minimum query. El mínimo del subintervalo $V[i, j]$ es el mínimo de los mínimos obtenidos para los subintervalos preprocesados que formen una partición de $V[i, j]$ . Por ejemplo, si $V = [3,2,8,5,6,1,7,4]$ :

$\min(V[2,7]) = \min\{\min(V[2,2]), \min(V[3,4]), \min(V[5,6]), \min(V[7,7])\} = \min\{2, 5, 1, 7\} = 1$

En lo que sigue estudiaremos cómo construir el segment tree (librándonos de la suposición $n= 2^m$ ) y probaremos que es posible realizar una consulta y actualizar el vector de forma eficiente. Sin embargo, antes debemos saber qué operaciones tienen que realizar los nodos del segment tree para que esto sea posible.

Nodos del segment tree

La información relativa a los subintervalos del tipo $V[k2^l, (k+1)2^l-1]$ debe almacenarse en un nodo. Los subintervalos $V[i,i]$ son los casos base y sus nodos formarán las hojas del segment tree. Los nodos deben mantener 3 operaciones:

Asignar la información correspondiente al nodo en el caso de que este sea una hoja del árbol.
Generar la información del nodo a partir de dos nodos cuyos subintervalos sean una partición del subintervalo actual. Esta operación se denomina merge.
Devolver la información del subintervalo que el nodo representa.

Una plantilla para un nodo del segment tree sería la siguiente:

# Template for a Segment Tree Node.
# A node contains the information related with a vector subinterval.
class SegmentTreeNode(object):

    # Init the node.
    # info = Subinterval information
    def __init__(self):
        self.info = None

    # Given the value of an array element,
    # build the information for this leaf.
    def assignLeaf(self, value):
        pass # Insert the code to build the leaf information

    # Merge the information of left and right
    # children to form the parent node information.
    def merge(self, left, right):
        pass # Insert the merge code

    # Return the information contained in this node.
    def getInfo(self):
        return self.info

En el caso del range minimum query asignar la información a una hoja es asignarle el valor de la componente y realizar un merge es tomar el mínimo de la información de los nodos left y right.

    def assignLeaf(self, value):
        self.info = value
    def merge(self, left, right):
        self.info = min(left.getInfo(), right.getInfo())

Veremos que para que la eficiencia de las dos operaciones soportadas por el segment tree sea logarítmica las operaciones anteriores deben ser realizadas en tiempo constante, como sucede para este problema.

Construcción del segment tree

La construcción del segment tree consiste en crear un árbol binario como el de la Imagen 1. Sin embargo, se puede conseguir una implementación más eficiente al darse cuenta de que el árbol binario es completo. Por tanto, podemos almacenarlo en memoria mediante un heap ². Esto es, embebemos el árbol en un vector mediante un recorrido por niveles como sucede en la Imagen 2. A cada nodo le corresponde un índice del vector y para estos índices se verifica:

$IndiceHijoIzquierda(nodo) =$ $2nodo$
$IndiceHijoDerecha(nodo) =$ $2nodo+1$

Estas relaciones nos permiten acceder a los hijos de forma constante. Además, la longitud del vector que representa al segment tree es $2n-1$ donde $n$ es la longitud de $V$ .

Imagen 2. Segment tree asociado a un vector $V$ de longitud 8 representado como un heap.

Nótese que el subintervalo correspondiente a cada nodo se deduce de su índice, por lo que no es necesario almacenar esta información. Se puede construir el árbol recursivamente. Si el nodo actual es una hoja se obtiene su información mediante el método assignLeaf. Si no se da este caso, se construyen recursivamente los dos hijos y se obtiene la información para el nodo actual aplicando el método merge a ambos hijos.

Con el proceso de construcción anterior obtendremos sin problemas el árbol aunque el vector no tenga como tamaño una potencia de dos. En tal caso el árbol resultante puede no ser completo. Por tanto, habrá componentes del heap en memoria sin usar. Esto nos es irrelevante puesto que el tamaño del heap será a lo sumo $2m-1$ donde $m$ es la menor potencia de 2 mayor que $n$ (si extendemos el vector con elementos nulos hasta que tenga longitud $m$ y construimos este heap necesitaremos un vector de longitud $2m-1$ ). Por tanto, la memoria utilizada será $\theta(n)$ en cualquier caso.

El siguiente código proporciona un constructor para la clase SegmentTree.

class SegmentTree(object):

    # Build a segment tree from the given array.
    # array: Array from which the segment tree is built.
    # st_index: current segment tree node index.
    # lo and hi : Range of input array subinterval that this node is responsible of.
    def _buildTree(self, array, st_index, lo, hi):
        if lo == hi:
            # The node is a leaf responsible of V[lo,lo]
            self.nodes[st_index].assignLeaf(array[lo])
        else:
            # The node is not a leaf.
            # Both children are built and merged afterwards for this node.
            left = 2 * st_index
            right = left + 1
            mid = (lo + hi) // 2
            self._buildTree(array, left, lo, mid)
            self._buildTree(array, right, mid + 1, hi)
            self.nodes[st_index].merge(self.nodes[left], self.nodes[right])

    # Get the segment tree size for a input of size N.
    # It compute the smallest 2 to the power of m greater than N.
    def _getSegmentTreeSize(N):
        size = 1
        while size < N:
            size <<= 1
        return size << 1

    # Initializes a Segment Tree.
    # array : Array from which the segment tree is built.
    # Node : Class that will be used as a segment tree node.
    #   It obtains the desired information from the array.
    def __init__(self, array, Node):
        self.SegmentTreeNode =  Node
        # Segment tree size (number of nodes)
        self.size = SegmentTree._getSegmentTreeSize(len(array))
        # Heap with the nodes
        self.nodes = [self.SegmentTreeNode() for i in range(0,self.size)]
        self.array = array
        # The tree is built
        self._buildTree(array, 1, 0, len(array)-1)

Como se construyen menos de $4n-1$ nodos, el proceso anterior es $\theta(n \max(a(n), m(n)))$ donde $a(n)$ es la eficiencia del método assignLeaf y $m(n)$ es la eficiencia del método merge.

En el caso del range minimum query la eficiencia obtenida es lineal como se había pronosticado.

Operación 1: Consultas

Para realizar una consulta debemos encontrar la descomposición de $V[i,j]$ en el menor número posible de nodos del árbol. Esto se puede consequir de forma recursiva. Partimos del nodo raíz. Se distinguen los siguientes casos:

Si $V[i,j]$ es el subintervalo que corresponde al nodo actual se devuelve la información contenida en el nodo.
Si $V[i,j]$ es un subintervalo del subintervalo del hijo izquierda se devuelve el resultado de la búsqueda obtenida para el hijo izquierda.
Si $V[i,j]$ es un subintervalo del subintervalo del hijo derecha se devuelve el resultado de la búsqueda obtenida para el hijo derecha.
Si $V[i,j]$ tiene elementos en ambos hijos se obtiene el valor de la consulta haciendo un merge de la información obtenida para el sector relativo al hijo izquierda y el sector relativo al hijo derecha.

El siguiente código realiza la operación descrita:

    # Get recursively a SegmentTreeNode with the information associated with the range [lo, hi].
    # st_index : Current Segment Tree Node. It is responsible of [left, right] range.
    def _getInfo(self, st_index, left, right, lo, hi):
        # Check if the range is the current node in the tree.
        # In that case return it.
        if left == lo and right == hi:
            return self.nodes[st_index]

        # Look for the range in the children of the current node
        # if it could be just there.
        mid = (left + right) // 2
        if lo > mid:
            return self._getInfo(2*st_index+1, mid+1, right, lo, hi)
        if hi <= mid:
            return self._getInfo(2*st_index, left, mid, lo, hi)

        # If we keep executing the method then the range is divided between
        # the left child and the right child of the current node. Let's get
        # each part of the range and merge it.
        left_result = self._getInfo(2*st_index, left, mid, lo, mid)
        right_result = self._getInfo(2*st_index+1, mid+1, right, mid+1, hi)
        result = self.SegmentTreeNode()
        result.merge(left_result, right_result)
        return result

    # Get the value associated with the range [lo, hi]
    def getInfo(self, lo, hi):
        result = self._getInfo(1, 0, len(self.array)-1, lo, hi)
        return result.getInfo()

Es claro que si el subintervalo es precisamente uno de los que se tienen almacenados en el árbol entonces el tiempo de la consulta es $O(\log n)$ . ¿Qué sucede en cualquier otro caso?

Proposición: El tiempo de consulta para cualquier subintervalo es $O(m(n)\log n)$ , donde $m(n)$ es la eficiencia del método merge.

Demostración

La implementación previa consiste en una búsqueda en profundidad pues es más cómoda de programar. Sin embargo, en la prueba es más útil ver el algoritmo como una búsqueda en anchura. Puesto que ambas búsquedas visitarían los mismos nodos, podemos situarnos en esta última. Definimos una iteración del algoritmo como procesar todos los nodos de un nivel $t$ del árbol. Tras una iteración los nodos que quedan activos pertenecen al siguiente nivel del árbol.

Buscamos la información del subintervalo $V[i,j]$ . Podemos observar que de una iteración a otra se mantiene la búsqueda sobre a lo sumo dos nuevos nodos. Además, estos nodos son precisamente aquellos cuyos subinvervalos contienen a las componentes i-ésima y j-ésima respectivamente.

En efecto, esto se prueba por inducción sobre el nivel del árbol en el que nos encontremos:

Para la raíz (nivel 1) esto es evidente pues el algoritmo, en el peor de los casos, prosigue con los dos hijos.
Supongamos cierta la afirmación para el nivel y veamos que se cumple para . Por la hipótesis de inducción, la búsqueda se mantiene a lo sumo en dos nodos. Si no hubiese nodos activos hemos terminado. Si por el contrario solo hubiese un nodo activo el resultado también es evidente (el nodo activo se divide como mucho en dos). Por último, si hay dos nodos activos verificando la hipótesis de inducción se tiene que (los nodos tienen subintervalos disjuntos). Cada uno de los nodos activos puede dividir la búsqueda como mucho sobre sus dos hijos. Para el nodo izquierda (el que contiene la componente ) se tienen las siguientes opciones:
- El subintervalo del nodo está contenido en $V[i,j]$ en cuyo caso se para la búsqueda en esa rama.
- El subintervalo que buscamos está contenido en el hijo derecha (tiene intersección vacía con el hijo izquierda). En tal caso se añade ese nodo a la búsqueda.
- El subintervalo que buscamos tiene intersección no vacía con el hijo izquierda. Entonces, este hijo se añade a la búsqueda. El subintervalo del hijo derecha está contenido en $V[i,j]$ (está acotado por $i$ y por $j$ ). Por tanto, no hay que continuar la búsqueda con el hijo derecha. Cuando finalice la búsqueda en el hijo izquierda se realizará un merge entre la información de ambos hijos.

En cualquier caso, se añade a lo sumo un hijo a la búsqueda. Lo mismo sucede con el nodo que contiene a $j$ , verificándose, por tanto, la afirmación.

Como consecuencia, el número de nodos que se visitan está acotado por $4 \log n$ . A cada nodo visitado le corresponde como mucho una operación de merge. Por tanto, la consulta es $O(m(n)\log n)$ .

$\tag*{$\blacksquare$}$

Nótese que para $V[1,n-2]$ con $n$ potencia de $2$ se realizan precisamente $\Omega(m(n)\log n)$ operaciones, luego la cota dada para la eficiencia del algoritmo es la mejor posible. Como pronosticábamos, si el merge es constante entonces la consulta es logarítmica.

Operación 2: Actualización de una componente del vector

Con la operación anterior ya habríamos resuelto la versión básica del range minimum query. Veamos que también podemos actualizar componentes del vector eficientemente y de forma sencilla.

En primer lugar, habría que actualizar la hoja correspondiente a la componente del vector. Después hay que arreglar los desperfectos que esto haya podido causar a sus antecesores. Para ello habrá que recorrer el camino que une la hoja con la raíz.

La implementación más sencilla de este proceso es recursiva. Realizamos una búsqueda en profundidad desde la raíz hasta la hoja correspondiente que actualizaremos mediante la operación assignLeaf. Posteriormente, se irán actualizando los antecesores en orden mediante operaciones merge de sus hijos, que ya están actualizados.

El siguiente código realiza la operación descrita:

    # Update the segment tree.
    # The given value is assigned to the array's component at index place.
    # The segment tree is updated accordingly in a recursive way.
    # st_index : Current segment tree node index.
    # lo and hi : The current range is [lo, hi]
    # index : Array's component to be updated.
    # value : New value for the array's component to update.
    def _update(self, st_index, lo, hi, index, value):
        # If current node is a leaf we have ended the search.
        # The value information is assigned to the leaf.
        if lo == hi:
            self.nodes[st_index].assignLeaf(value)

        # If the current node is not a leaf, the search continues recursively
        # and the current node information is updated afterwards.
        else:
            left = 2 * st_index
            right = left + 1
            mid = (lo + hi) // 2
            # Continue the search by the correct path
            if index <= mid:
                self._update(left, lo, mid, index, value)
            else:
                self._update(right, mid+1, hi, index, value)
            # Update current node information
            self.nodes[st_index].merge(self.nodes[left], self.nodes[right])

    # Update the segment tree.
    # The given value is assigned to the array's
    # component at index place. The segment tree is updated accordingly.
    # index : Array's component to be updated.
    # value : New value for the array's component to update.
    def update(self, index, value):
        self._update(1, 0, len(self.array)-1, index, value)
        self.array[index] = value

La eficiencia es claramente $\theta(m(n) \log n + a(n))$ .

Una mejor implementación es una versión iterativa del proceso. Comenzamos en la hoja y recorremos el camino desde esta a la raíz usando el siguiente hecho:

$IndicePadre(nodo) = \frac{nodo}{2}$

Si en determinado momento la información de un nodo a actualizar no cambia con el merge se finaliza algoritmo. Sin embargo, aunque podamos terminar la ejecución antes, la eficiencia en el peor caso sigue siendo $\theta(m(n) \log n + a(n))$ . Se necesitaría, además, un nuevo método isSameInfo que nos indique si la información que se le pasa como argumento es la misma que la contenida por el nodo. Este método debe ser $O(m(n))$ para que la implementación sea rentable. El siguiente código contiene esta nueva versión del algoritmo:

    # Update the segment tree.
    # The given value is assigned to the array's
    # component at index place. The segment tree is updated accordingly.
    # index : Array's component to be updated.
    # value : New value for the array's component to update.
    def update2(self, index, value):
        st_index = self.size // 2 + index # Leaf index
        # Update leaf and array
        self.array[index] = value
        self.nodes[st_index].assignLeaf(value)
        # Update leaf ancestors
        st_index = st_index // 2
        while st_index > 0:
            # Get current info and update it with a merge from the children
            current_info = self.nodes[st_index]
            self.nodes[st_index].merge(self.nodes[2*st_index], self.nodes[2*st_index+1])
            # If the info has not changed then the algorithm ends
            if self.nodes[st_index].isSameInfo(current_info):
                break
            # Go to node's parent
            st_index = st_index // 2

Problemas

Los siguientes problemas son útiles para practicar con los segment trees.

Dado un vector $V$ con $N$ elementos, se pide realizar $Q$ consultas. Cada consulta consiste en obtener la media del subintervalo $V[i,j]$ . Desarrollar un algoritmo para este cometido.
Dado un vector $V$ con $N$ elementos, se pide realizar $Q$ consultas. Cada consulta consiste en obtener la suma de los elementos del subintervalo $V[i,j]$ . Encontrar una estructura de datos con preprocesamiento lineal y tiempo de consulta constante (diferente al segment tree) que resuelva el problema. ¿Es válida la solución si en lugar de la suma se utilizase la operación OR lógica de los números en binario? ¿Por qué? Extender el algoritmo a este último caso, estudiar las nuevas eficiencias obtenidas y compararlas con las de una solución basada en segment trees.
Hackerrank - Functional Programming Contest - Range Minimum Query
Hackerrank - Minimum Product Subinterval
90 Segment Trees Problems

Código

Todo el código proporcionado se encuentra en un único archivo en Python. Una implementación similar se puede encontrar en C++ ³.

Para profundizar

Los siguientes enlaces profundizan en la temática. Incluyen desde operaciones más avanzadas, como el uso de lazy propagation, hasta la relación del range minimum query con otros problemas, como el lowest common ancestor. Espero tratar estos temas en un futuro próximo.

Segment trees y Range minimum query